excuse me, i just realized that the height of the sun to touch the horizon should be 0.25° not 0.5°, since 0.5° is the angular diameter, not the radius. that correction would make the previous math even more damning for the flat earth model.
[HR][/HR][HR][/HR]
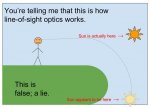
if the sun is actually 3,239 miles up, how far away would it have to be for perspective to explain it appearing to be 0.25° above the horizon?
((i.e. -- just touching the horizon at midnight -- still never setting or rising: that is still utterly impossible on a flat earth))
solve:
tan(3239/x) = 0.25°
3239/x = tan(0.25°)
x = 3239/tan(0.25°)
x = 742,319 miles
[HR][/HR][HR][/HR]
you need a much bigger frisbee, dude.
but it can never be big enough to explain a sunset or a sunrise.
[HR][/HR][HR][/HR]
if the sun is actually 3,239 miles up, how far away would it have to be for perspective to explain it appearing to be 0.25° above the horizon?
((i.e. -- just touching the horizon at midnight -- still never setting or rising: that is still utterly impossible on a flat earth))
solve:
tan(3239/x) = 0.25°
3239/x = tan(0.25°)
x = 3239/tan(0.25°)
x = 742,319 miles
[HR][/HR][HR][/HR]
you need a much bigger frisbee, dude.
but it can never be big enough to explain a sunset or a sunrise.
Last edited: