You are simply displaying your complete inability to understand anything outside of your preconceived, ridiculous notions. I'll say it again, in a way that even you might be able comprehend: If the earth was flat, the only limit to radar detection range would be the available power.
Did you read the article that I posted about radar on ships? Obviously not. The longest range they quoted was 9 nautical miles. That's about 17 km. It assumes a radar mounted above sea level and a large vessel such as a cargo ship as the target.
Australia has a radar system that can see over the horizon, for thousands of kilometers. It works by bouncing signals off the ionosphere. If the earth was flat, there would be no need for it.
I made it *really* simple. Not so much for you, because I think you are shilling for ball-Earth, rather than genuinely trying to understand. But for anyone honest that reads your posts and for whatever reason believes you might be right.
https://www.quora.com/What-is-the-range-of-an-average-marine-radar-on-US-Navy-ships?share=1
"Almost every one of the 50+ US Navy ships I sailed on had an installed “average marine radar” from a manufacturer like Raytheon or Furuno. These tend to be “fishing boat” radars with ranges of 25 to 75 nm, depending on how high above the sea surface they were installed."
Note that 25 nautical miles (the lower estimate given) is approximately 46km.
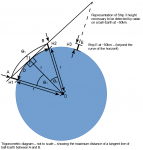
● Let A, B and E represent 3 ships, of height H1, H2, H3, on a ball-Earth of circumference C and radius r.
● Let ships A and B be located on the ball-Earth at such a distance that a straight line between the highest point on A and the highest point on B is tangent with ball-Earth. [This sets ship B at the maximum possible detectable distance, by straight line, from A].
● Let T represent the point where the tangent line AB intersects the ball-Earth.
● Let O represent the center of ball-Earth.
● Let ϴ1 represent the angle between OA and OT.
● Let ϴ2 represent the angle between OT and OB.
● Let ϴT represent the sum of the angles ϴ1 and ϴ2.
● Let D represent the distance of the arc along the circumference of ball-Earth, between the ships A and B.
Also, let:
● H1 = 10m
● H2 = 10m
● C = 40,075,017m
● r = 6,378,000m
Then:
● From basic trigonometry, we know that cos(ϴ) = Adjacent/Hypotenuse
cos (ϴ1) = r / (r + H1)
cos (ϴ1) = 0.999998432112838
cos (ϴ2) = r / (r + H2)
cos (ϴ2) = 0.999998432112838
ϴ1 = acos(0.999998432112838)
ϴ1 = 0.00177081200133473 radians
ϴ2 = acos(0.999998432112838)
ϴ2 = 0.00177081200133473 radians
● We also know that 360º = 2π radians
ϴ1 = 0.001770812 * 360 / (2.π)
ϴ1 = 0.101460053987595º
ϴ2 = 0.001770812 * 360 / (2.π)
ϴ2 = 0.101460053987595º
ϴT = ϴ1 + ϴ2
ϴT = 0.10146º + 0.10146º
ϴT = 0.20292º
● There are 360º in a circle.
D = ϴT / 360 * C
D = 0.20292º / 360º * 40,075,017m
D = 22588.951249m
D = 22.59km
● Therefore, if we lived on a ball-Earth of circumference C = 40,075km, the maximum range that a straight‑beam radar mounted 10m above sea-level could detect a 10m-high ship, is 22.59km.
● In reality, radar can detect ships at much greater distances than this (e.g. easily at 50km).
● The trigonometric diagram of ball-Earth, together with radar ranges which greatly exceed the maximum range predicted by the ball-Earth model, therefore demonstrate that we do not live on a ball‑Earth at all, as some would have us imagine.


